标题有点绕，简单来说就是有一些组合，类似【1，2】【2，3】【3，5】这种最终能够连成【1-5】，当然顺序可能是随机打乱的而且前后2个数字可能相等或者或大或小，需要判断能否找到一个有效的队列确保他们能连续衔接起来。这个题目的来源是我们做了个会员积分日志表，每获得或消费一笔积分都会在表里面记录操作前的剩余积分和操作后的剩余积分，因为积分是区分渠道和有效期的，所以也就存在同一个订单产生的积分日志有多条的情况，那么我们需要确保这些操作前后扣减的积分余量是正确的，否则可能存在积分日志的剩余积分数不准确的情况。在测试时当然可以通过人为去查库去判断日志的正确性，那么有没有办法让程序去判断呢？本文就以python为例结合我的解决过程来聊下（先说明下测试代码是先写的，里面配的原理图是写文章的时候现画的思路与当时写代码的会有点出入，介意的可以直接看原理图即可）。

花了一天半的时间，最后半天突然灵光一闪想到了一个秒解的方案，放到文章的最后了。

一、尝试方法 1，首位循环匹配+匹配失败的队列 递归再匹配

在拿到待匹配队列（判断是否能够最终连续的队列）时，取第一个元素作为第一个匹配成功的队列，后续的元素循环判断是否能够与“已匹配成功的结果”的左侧 或右侧匹配成功（比如现在成功的是【1-5】，如果下一个待匹配的是【10，1】那么就是左匹配成功，结果就是【10-5】；如果下一个是【5，7】那么则是右匹配成功，结果就是【1，7】）；

匹配过程中失败的需要记录下来，等待匹配的循环结束后，需要把失败的记录作为待匹配的记录进行下一个递归调用，直到输入的【待匹配组合】与循环结束后的【失败记录】元素匹配，则说明这个无序组合确实不能匹配成功。下面是大致的原理图：

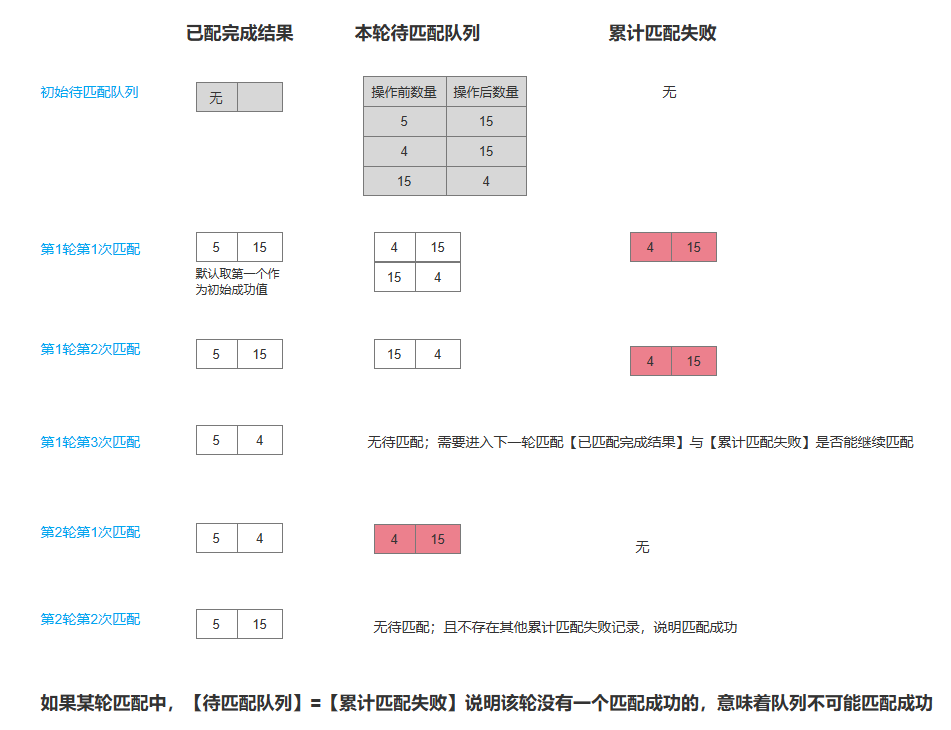
下面附上当时的python测试代码：

def check(list_ori, list_mid, times=30, line=''):
    list_other = []
    # list_mid = []
    times -= 1
    # print(list_ori)
    for k in list_ori:
        # print(k)
        # print(f"操作前list_mid={list_mid}; 此时获取的list_ori={k}")
        if len(list_mid) == 0:
            # list_mid[0] = list_ori[k][0]
            # list_mid[1] = list_ori[k][1]
            # list_mid.append([k[0], k[1]])
            list_mid = [k[0], k[1]]
            line += f"开始:【{k[0]},{k[1]}】"
        else:
            if list_mid[0] == k[1]:
                list_mid[0] = k[0]
                line += f" -->[{k[0]},{k[1]}] =【{list_mid[0]},{list_mid[1]}】"
            elif list_mid[1] == k[0]:
                list_mid[1] = k[1]
                line += f" -->[{k[0]},{k[1]}] =【{list_mid[0]},{list_mid[1]}】"
            else:  # 2者比较，左右都不能形成连续性的，暂存到其他列表
                list_other.append([k[0], k[1]])
        # print(f"操作后list_mid={list_mid} ； list_other={list_other}")
    # print("=================== 本轮list_ori 循环结束 ===================")
    if times < 0:  # 超过允许递归的次数
        # print('20次内没有匹配成功')
        return 0, list_mid, '失败！！！' + line + ' 无法衔接的区间为：' + str(list_other)
    if len(list_other) == 0:
        # print('成功')
        return 1, list_mid, line
    else:
        return check(list_other, list_mid, times, line)

list_ori = [[5, 15], [4, 15], [15, 4]]

x = check(list_ori,[])
print(f"check={x[2]}")

但是后面验证的时候发现，这种算法解决不了下面这种组合，原因在于对于无序组合 可能存在2个元素首/尾匹配场景>1的情况，也就是【5，10】与【10，100】能匹配成功，但是【5，10】与【10，15】也能匹配成功，在下面的场景中显然如果先把【5-100】的结果匹配出来，那么后面怎么都不能匹配成功了：

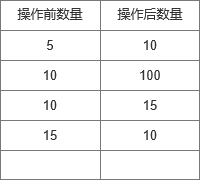
二、增加冲突组合队列，匹配组合必须不存在于冲突队列才可进行匹配判断

简而言之就是在方法1的基础上，把那些上一次匹配成功 但是后面递归时却最终匹配失败的情况，把当时匹配成功的队列组合标记为冲突队列，意在记录这些所谓匹配成功的情况最终会失败，所以遇到冲突队列相匹配的情况，需要挪到匹配失败那边去，以让给后面可能存在的其他匹配组合场景。下面是大致的原理图：

下面是测试python代码（请忽略里面的无效代码）：

import sys  # 导入sys模块
import time
from copy import deepcopy
sys.setrecursionlimit(3000)  # 将默认的递归深度修改为3000

# 原始list   本次待检测list   中间拼接list     冲突组合list  次数（应该可以不要）  字符串拼接（函数匹配的路径流线图）
def check3(list_ori, list_prep=None, list_mid=None, list_conflict=None, times=0,
           line=''):  # 序号递归、遍历， 待判断的list越长越消耗运算（匹配顺利的话 也很快）
    # 原始长度为1 返回正确
    try_times = 2000000
    if list_conflict is None:
        list_conflict = []
    if list_mid is None:
        list_mid = []
    if list_prep is None:
        list_prep = list(list_ori)
    # print(f"{times}、函数已进入，list_prep={list_prep}")
    # print(f"{times}、函数已进入，list_mid={list_mid}")
    # print(f"{times}、函数已进入，list_conflict={list_conflict}")
    list_other = []

    list_mid_before = list(list_mid)
    # print(list_ori)
    # list_prep_tmp = list(list_prep)
    list_prep_tmp = deepcopy(list_prep)
    for k in list_prep:  # 这里不能用list_prep_tmp来循环
        times += 1
        # print(k)
        # 关键操作
        # if [k[1], k[0]] in list_prep or k[1] == k[0]:  # 如果把[5,3]变换成[3,5]还存在与list_prep里面，则说明存在对称元素，需要消除偶数个对数
        #    list_prep.remove([k[1], k[0]])
        #    list_prep.remove(k)
        #    continue
        # 关键操作

        # print(f"操作前list_mid={list_mid}; 此时获取的list_ori={k}")
        if len(list_mid) == 0:
            # list_mid[0] = list_ori[k][0]
            # list_mid[1] = list_ori[k][1]
            # list_mid.append([k[0], k[1]])
            list_mid = [[k[0], k[1]], [[1, 1]], [k[0], k[1]]]  # 【已知的组合，已知组合的上次组合list链条，已知组合本次组合的list】
            line += f"rn=开始:【{k[0]},{k[1]}】" + "rn"
            list_mid_before = list(list_mid)

        else:
            # print(f"判断是否正在匹配冲突项目：{[list_mid[1],k]}             已知冲突项： {list_conflict}")
            list_mid0 = list(list_mid[1])
            list_mid0.append(list_mid[2])
            # print(f"判断是否正在匹配冲突项目：{[list_mid0, k]}             已知冲突项： {list_conflict}")
            # if [list_mid[1],k] not in list_conflict:#只有待匹配组合的 list链条 不是冲突list的子集才可以继续
            if [list_mid0, k] not in list_conflict:
                if list_mid[0][0] == k[1]:
                    list0 = list(list_mid[2])  # 只要匹配上了， 永远把上次最后一个匹配的值 追加到 追溯链中
                    list_mid[1].append(list0)  # 记录 上次组合结果，及本次入列组合成功的list

                    list_mid[2] = list(k)  # 只要匹配上 永远取最新匹配的这个值
                    list_mid[0][0] = k[0]
                    line += f"->入列【{k[0]},{k[1]}】  组合成功：{list_mid[0][0]},{list_mid[0][1]}      "
                elif list_mid[0][1] == k[0]:
                    list0 = list(list_mid[2])
                    list_mid[1].append(list0)
                    list_mid[2] = list(k)
                    list_mid[0][1] = k[1]
                    line += f"->入列【{k[0]},{k[1]}】  组合成功：{list_mid[0][0]},{list_mid[0][1]}      "
                else:  # 2者比较，左右都不能形成连续性的，暂存到其他列表
                    list_other.append([k[0], k[1]])
            else:  # 如果匹配上冲突了，那么要把本次待匹配的list 转移到其他list用于下一次递归

                list_other.append([k[0], k[1]])
        # print(f"操作后list_mid={list_mid} ； list_other={list_other}")
    # print("=================== 本轮list_ori 循环结束 ===================")
    if times > try_times:  # 超过允许递归的次数
        # print('20次内没有匹配成功')
        return 0, list_mid, f"已失败{times}次，超过预设值{try_times}！！！  无法衔接的区间为：{list_other}"

    if len(list_other) == 0:
        # print(f'成功,尝试了{times}次')
        return 1, list_mid, f'成功,尝试了{times}次'
    else:

        if len(list_ori) - len(list_other) == 1:  # 待匹配原始list 比 无法完成匹配list 多一个（多的是给首次list_mid赋值的那个）
            # print(f"失败！ 尝试次数{times}")
            print(f"{list_ori}----{list_other}")
            return 0, list_mid, f"失败了！ 尝试次数{times}"

        if list_ori == list_prep and times > len(list_ori):  # 这里不进行返回判定 可能也不会造成死循环了，因为某些情况下会全部初始化重新跑一遍（但是冲突list 是不会重置的）
            print(f"{list_ori}----{list_prep}----{times}")
            # print(f"已全部递归完毕，失败！！！ 尝试{times}次")
            # return 0, list_mid, f"已全部递归完毕，失败！！！ 尝试{times}次"

        # 本次大循环 list_mid 没有获得任何匹配，则说明本次大失败;上次决定的list_mid虽然匹配，但是往下（也就是在本次大循环中）无法匹配成功
        # print(f"list_imd={list_mid}   list_mid_before={list_mid_before}")
        if list_mid == list_mid_before and [list_mid[1], list_mid[2]] not in list_conflict:
            list_conflict.append([list(list_mid[1]), list(list_mid[2])])
            print(f"1 号递归{times}rn")
            print(f" list_ori={list_ori} rn")
            print(f" list_prep={list_prep} rn ")
            print(f" list_mid={list_mid} rn ")
            # return check3(list_ori, list_ori, [], list_conflict, times, line)  # 全部重新来计算，只是多了一个冲突组合
            # 这一轮，一个都没匹配上，那么应该 是上一个正确匹配的是冲突项，需要回退一个匹配层级
            return check3(list_ori, list_prep.append(list_mid[2]), [], list_conflict, times, line)
        else:
            # print("*************list_mid 与list_mid_before 不匹配******************")
            # 如果在里面的话，说明还要再往上一级取冲突组合（那个冲突组合也是可以 组合的）
            list_conflict.append([list(list_mid[1][:-1]), list(list_mid[1][-1])])
            pass

        # 这里面需要有个逻辑处理 最终匹配失败的情形， 失败可能原始list 没有任何2 2可以组合的情况，所以list_prep无论如何都不会出现=1的情况
        if len(list_prep) == 1:  # 说明待检测的是最后一个了,而且还没匹配成功

            # list_conflict.append([list_mid,list_prep])#应该匹配上一次的比对成功的组合（该组合也可能不存在）！
            if list_mid[1][0][0] != 'no':
                list_conflict.append([list_mid[1], list_mid[2]])
            # print("2 号递归rn")
            return check3(list_ori, list_ori, [], list_conflict, times, line)  # 全部重新来计算，只是多了一个冲突组合--->这里可能导致直接判定失败
        else:
            # print("3 号递归rn")
            return check3(list_ori, list_other, list_mid, list_conflict, times, line)

list_ori2 = [5, 10], [10, 100], [10, 15],[15,10]
x = check3(list_ori2)
print(f"check={x[2]}")

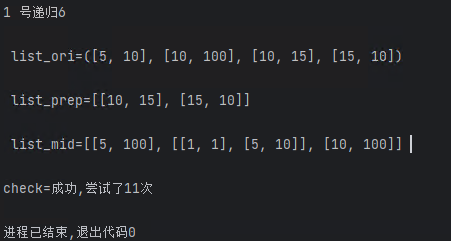
这个算法类似于穷举法，所以如果无序的组合越多顺序越乱那么可能需要尝试的次数就越多，好处是如果成功可已提取出成功的组合方式。

三、首位消消乐，一秒解决问题

在体会到第二种方式的效率后，突然想到这个问题无非就是判断是否能够首尾串联起来嘛！那么我们可以倒推下，如果一系列无序组合最终能够串联起来，那么必然最终的正确结果必然存在”首“与”尾“，也就是中间那些”首“跟”尾“必然可以消除掉！就像下面这样：

那么就很简单了，我们把每个元素的首与尾拆分开来，然后进行消除，最终看下剩余情况即可。

因为首与尾都是成对的，所以只要看一边的剩余元素就可以了（注意消除的时候要一个个消除，比如左边出现5，那么消除的时候应该左边消除一个5，右边消除一个5，不能把都是5的全部消除了！），下面上python代码:

from copy import deepcopy

def check4(list_ori):  # 这种方法简单高效
    list_left = []
    list_right = []
    for k in list_ori:
        list_left.append(k[0])
        list_right.append(k[1])
    # print(f"list_left={list_left}")
    # print(f"list_right={list_right}")
    # list_left_tmp=list(list_left)
    list_left_tmp = deepcopy(list_left)
    for v in list_left_tmp:  # 如果在list_left本体进行for循环，那么就会导致一边删除一边循环，下标会偏移
        # print(f"v={v}  list_left={list_left}")
        if v in list_right:
            list_right.remove(v)
            list_left.remove(v)
            # print(f"删除v={v}  删除后list_left={list_left}")
            continue
    if len(list_left) > 1:

        return 0, 0, '失败'
    else:

        return 1, 1, '成功'

list_ori2 = [5, 10], [10, 100], [10, 15],[15,10]
x = check4(list_ori2)
print(f"check={x[2]}")

好了，这个算法题就此结束，可能大神一下就能想到快速高效的解决办法吧，如果朋友们有自己写的其他算法，可以用我下面的这些例子去跑一下（这些都是我当时测验时用的），看看结果是否正确。

    list_ori = [[1, 10], [7, 10], [2, 7], [10, 2]]
    list_ori = [[1, 10], [7, 10], [2, 70], [10, 2], [10, 1], [2, 7]] 
    list_ori = [[1, 100], [2, 50], [1, 2], [50, 100], [100, 1]]
    list_ori = [[1, 5], [5, 500], [5, 20], [20, 5], [500, 999]]  
    list_ori = [[1, 5], [5, 500], [5, 20],[20, 5]]  # 这个list 无法通过第一次检测函数 因为1，5  5，500；是这个冲突项，实际也会在正确序列中出现！
    list_ori = [[5, 20], [1, 5], [5, 500], [20, 5]]
    list_ori = [[1, 3], [3, 10], [3, 5], [5, 6], [6, 3]]  # 这个是可以匹配出结果的

    list_ori = [[1, 3], [100, 1], [2, 22], [2, 9], [3, 2]]  
    list_ori = [[1, 2], [3, 8], [2, 100], [50, 100], [1, 3]] 
    list_ori = [[1, 3], [21, 9], [3, 2]]  
    list_ori = [1, 2], [2, 3], [3, 8], [8, 1000], [1, 2], [2, 3], [3, 8], [8, 7], [7, 1000], [1000, 1], [1, 2], [2,33], [33, 8], [8, 7], [7, 1000], [1000, 1]  # 这个可以
    # list_ori = [1, 2], [2, 3], [3, 8], [8, 1000], [1, 2], [2, 3], [3, 8], [8, 7], [7, 1000], [1000, 1], [1, 2], [2, 33], [ 33, 8], [8, 7], [7, 1000], [1000, 2]  # 循环跳不出来？？？？？？
    list_ori = [2, 3], [1, 2], [1, 2], [2, 3], [3, 8], [8, 1000], [1, 2], [2, 3], [3, 8], [8, 7], [7, 1000], [1000,1], [1,2], [2, 33], [33, 8], [8, 7], [7, 1000], [1000, 1], [3, 8], [8, 1000], [1, 2], [2, 3], [3, 8], [8, 7], [7, 1000], [1000, 1], [1, 2], [2, 33], [33, 8], [8, 7], [7, 1000], [1000, 2]  # 循环跳不出来？？？？？？
    

基于互联网精神，在注明出处的前提下本站文章可自由转载！

本文链接：https://ranjuan.cn/python-list-order-check/